
Toán 7 Bài 16: Tam giác cân. Đường trung trực của đoạn thẳng
Câu hỏi trang 80 Toán 7 Tập 1:
Hãy nêu tên tất cả các tam giác cân trong Hình 4.59. Với mỗi tam giác cân đó, hãy nêu tên cạnh bên, cạnh đáy, góc ở đỉnh, góc ở đáy của chúng.
Hướng dẫn giải
Tam giác ABC có AB = AC = 3 cm
=> Tam giác ABC cân tại A.
Trong tam giác cân ABC có:
Cạnh bên: AB, AC
Cạnh đáy: BC
Góc ở đáy: 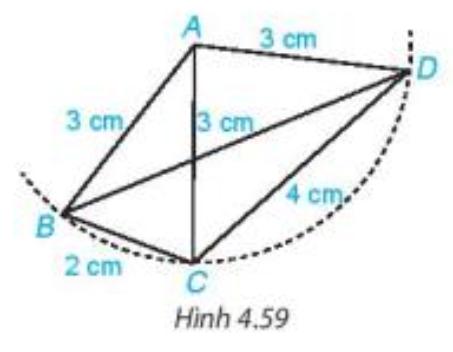 (widehat {ABC};widehat {ABC})
(widehat {ABC};widehat {ABC})
Tam giác ADC có AD = AC = 3 cm
=> tam giác ADC cân tại A.
Trong tam giác cân ADC có:
Cạnh bên: AD, AC.
Cạnh đáy: CD.
Góc ở đỉnh: (widehat {DAC})
Góc ở đáy: 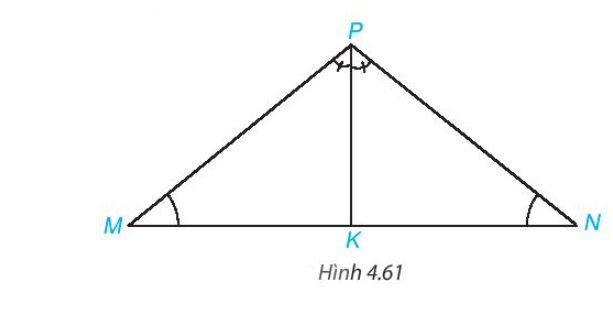 (widehat {ACD};widehat {ADC})
(widehat {ACD};widehat {ADC})
Tam giác ABD có AB = AD = 3 cm nên tam giác ABD cân tại A.
Trong tam giác cân ABD có:
Cạnh bên: AB, AD.
Cạnh đáy: BD.
Góc ở đỉnh: (widehat {DAB})
Góc ở đáy: (widehat {ACD};widehat {ADB})
HĐ1 trang 81 Toán 7 Tập 1:
Quan sát tam giác ABC cân tại A như Hình 4.60. Lấy D là trung điểm của đoạn thẳng BC.
a) Chứng minh rằng ΔABD = ΔACDtheo trường hợp cạnh - cạnh - cạnh.
b) Hai góc B và C của tam giác ABC có bằng nhau không?
Hướng dẫn giải
a) Xét hai tam giác ABD và ACD có:
AB = AC (do tam giác ABC cân tại A)
AD chung
BD = CD (do D là trung điểm của đoạn thẳng BC)
=> ΔABD = ΔACD (c - c - c)
b) Ta có: ΔABD = ΔACD
=> (widehat {ABD} = widehat {ACD}) hay 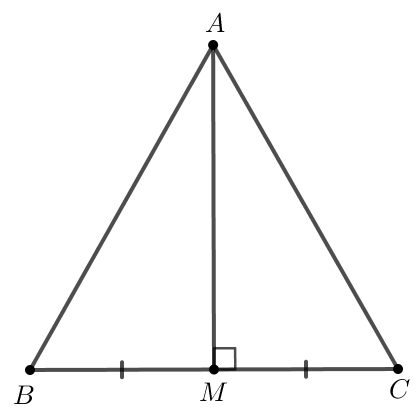 (widehat {ABC} = widehat {ACB})
(widehat {ABC} = widehat {ACB})
HĐ2 trang 81 Toán 7 Tập 1:
Cho tam giác MNP có (widehat M = widehat N). Vẽ tia phân giác PK của góc MPN (K ∈ MN).
Chứng minh rằng:
a) (widehat {MKP} = widehat {NKP})
b) ΔMPK = ΔNPK
c) Tam giác MNP có cân tại P không?
Hướng dẫn giải
a) Xét tam giác MPK ta có:
(begin{matrix} widehat {MPK} + widehat {PMK} + widehat {MKP} = {180^0} hfill Rightarrow widehat {MKP} = {180^0} - left( {widehat {MPK} + widehat {PMK}} right) hfill end{matrix})
Xét tam giác NPK ta có:
(begin{matrix} widehat {NPK} + widehat {PNK} + widehat {NKP} = {180^0} hfill Rightarrow widehat {NKP} = {180^0} - left( {widehat {NPK} + widehat {PNK}} right) hfill end{matrix})
Mà PK là tia phân giác của góc MPN
=> (widehat {MPK} = widehat {NPK})
Mặt khác (widehat {PMK} = widehat {PNK}) (gt)
=> (widehat {MKP} = widehat {NKP})
b) Xét tam giác MPK và tam giác NPK ta có:
PK là cạnh chung
(widehat {MPK} = widehat {NPK})
(widehat {MKP} = widehat {NKP})
=> (Delta MPK = Delta NPKleft( {g - c - g} right))
c) Do ΔMPK = ΔNPK=> PM = PN (hai cạnh tương ứng).
Tam giác MNP có:
PM = PN
=> Tam giác MNP cân tại P
Vậy tam giác MNP cân tại P
Luyện tập 1 trang 81 Toán 7 Tập 1:
Tính số đo các góc và các cạnh chưa biết của tam giác DEF trong Hình 4.62.
Hướng dẫn giải
Tam giác FDE có FD = FD = 4 cm
=> Tam giác FDE cân tại F
=> (widehat D = widehat E = {60^0})
Xét tam giác FDE có
(begin{matrix} widehat D + widehat E + widehat F = {180^0} hfill Rightarrow widehat F = {180^0} - left( {widehat D + widehat E} right) hfill Rightarrow widehat F = {180^0} - left( {{{60}^0} + {{60}^0}} right) = {60^0} hfill end{matrix})
Xét tam giác DEF có:
(widehat F = widehat E = {60^0})
=> Tam giác DEF cân tại D
=> DE = DF = 4 cm
Bài 4.23 trang 84 Toán 7 Tập 1
Cho tam giác ABC cân tại A và các điểm E, F lần lượt nằm trên các cạnh AC, AB sao cho BE vuông góc với AC, CF vuông góc với AB (H.4.69). Chứng minh rằng BE = CF.
Hướng dẫn giải:
Do tam giác ABC cân tại A nên:  (widehat {ABC} = widehat {ACB}) (tính chất tam giác cân)
(widehat {ABC} = widehat {ACB}) (tính chất tam giác cân)
Xét 2 tam giác vuông BFC và CEB:
 (widehat {ABC} = widehat {ACB})
(widehat {ABC} = widehat {ACB})
BC chung
Delta BFC = Delta CEB' width='174' height='17'>(=>Delta BFC = Delta CEB) (cạnh huyền - góc nhọn)
=>BE = CF (2 cạnh tương ứng).
Bài 4.24 trang 84 Toán 7 Tập 1
Cho tam giác ABC cân tại A và M là trung điểm của đoạn thẳng BC. Chứng minh AM vuông góc với BC và AM là tia phân giác của góc BAC.
Hướng dẫn giải:
Xét 2 tam giác AMC và AMB có:
AM chung
AB = AC (do tam giác ABC cân tại A)
MB = MC (gt)
(Rightarrow Delta AMB=AMC(c.c.c))
(Rightarrow widehat {CAM} = widehat {CBM}) (2 góc tương ứng)
(Rightarrow AM) là phân giác của góc BAC
Mặt khác:(widehat {AMB} = widehat {AMC}) (2 góc tương ứng) mà (widehat {AMB} + widehat {AMC} = {180^o}) (2 góc kề bù)
Nên: (widehat {AMB} = widehat {AMC} = {90^o}).
Vậy AM vuông góc với BC.
Bài 4.25 trang 84 Toán 7 Tập 1
Cho tam giác ABC và M là trung điểm của đoạn thẳng BC.
a) Giả sử AM vuông góc với BC. Chứng minh rằng tam giác ABC cân tại A.
b) Giả sử AM là tia phân giác của góc BAC. Chứng minh rằng tam giác ABC cân tại A.
Hướng dẫn giải:
a.
Do M là trung điểm của BC nên MB = MC.
Do (AM⊥BC) nên tam giác AMB vuông tại M, tam giác AMC vuông tại M.
Xét hai tam giác AMB vuông tại M và AMC vuông tại M có:
AM chung.
MB = MC (chứng minh trên).
Do đó (ΔAMB=ΔAMC) (2 cạnh góc vuông).
Khi đó AB = AC (2 cạnh tương ứng).
Tam giác ABC có AB = AC nên tam giác ABC cân tại A.
Vậy tam giác ABC cân tại A.
b)
Kẻ MH vuông góc với AB (H thuộc AB)
MG vuông góc với AC (G thuộc AC)
Xét 2 tam giác vuông AHM và AGC có:
(widehat {HAM} = widehat {GAM})
AM chung
Delta AHM = Delta AGC' width='183' height='17'>(=>Delta AHM = Delta AGC) (cạnh huyền - góc nhọn)
=> HM = GM (2 cạnh tương ứng)
Xét 2 tam giác vuông BHM và CGM có:
BM=CM(gt)
MH=MG(cmt)
Delta BHM = Delta CGM' width='188' height='17'>(=>Delta BHM = Delta CGM) (cạnh huyền - cạnh góc vuông)
widehat {BMH} = widehat {CMH}' width='159' height='23'>(=>widehat {BMH} = widehat {CMH}) (2 góc tương ứng)
=> Tam giác ABC cân tại A.
Bài 4.26 trang 84 Toán 7 Tập 1
Tam giác vuông có hai cạnh bằng nhau được gọi là tam giác vuông cân.
Hãy giải thích các khẳng định sau:
a) Tam giác vuông cân thì cân tại đỉnh góc vuông;
b) Tam giác vuông cân có hai góc nhọn bằng 45°;
c) Tam giác vuông có một góc nhọn bằng 45° là tam giác vuông cân.
Hướng dẫn giải:
a. Dựa vào định lý tổng ba góc trong 1 tam giác bằng(180^{circ}) => tam giác không thể có 2 góc vuông
=>Tam giác vuông cân sẽ có 2 góc nhọn bằng nhau
=> Tam giác vuông cân thì cân tại đỉnh góc vuông.
b. Tam giác vuông cân sẽ có 2 góc nhọn bằng nhau => Tổng hai góc nhọn sẽ bằng : (180^{circ}- 90^{circ} = 90^{circ})
=> Mỗi góc nhọn sẽ là (45^{circ})
Vậy tam giác vuông cân có hai góc nhọn bằng 45°.
c. Áp dụng định lý tổng ba góc trong 1 tam giác bằng 180^{circ} , ta có số đo góc còn lại là : (180^{circ}- 90^{circ} - 45^{circ} = 45^{circ})
Vậy tam giác vuông có một góc nhọn bằng 45° là tam giác vuông cân.
Bài 4.27 trang 84 Toán 7 Tập 1
Trong Hình 4.70, đường thẳng nào là đường trung trực của đoạn thẳng AB?
Link nội dung: https://khoaqhqt.edu.vn/bai-16-tam-giac-can-duong-trung-truc-cua-doan-thang-a57902.html